Abstract

Playing chess is one of the first sectors of human thinking that were conquered by computers. From the historical win of Deep Blue against chess champion Garry Kasparov until today, computers have completely dominated the world of chess leaving no room for question as to who is the king in this sport. However, the better computers become in chess the more obvious their basic disadvantage becomes: Even though they can defeat any human in chess and play phenomenally great and intuitive moves, they do not seem to know what chess it. Recently, the advent of AlphaZero brought the level of computers to even higher grounds, but made that disadvantage even more obvious. Nowadays the best chess algorithm can find the best moves in any position without having any knowledge of any chess principle whatsoever. A new world of capabilities and knowledge lays open in front of us, but the darkness behind it is deeper than we could ever imagine. The neural network algorithms seem capable of being best in something without even knowing what that something is, making questions regarding the essence of what thought is more important than ever.

Goals of this paper

This paper aims at unveiling the major issue of Artificial Intelligence (AI) today, which is the inability of neural networks to actually know what they talk about. The field of chess algorithms will be used as a basis for this analysis, although the implications of the findings have far broader consequences than just the world of chess. The need to re-define what (chess) knowledge is, is one of the major needs as a result of the analysis documented below. A paradigm shift of how humans view artificial intelligence is also highlighted, although the full complications of such a shift go beyond the goals of this paper.

Chess algorithms – An Overview

In chess programming there are two major strategies that can be followed. These strategies were first documented by the computer programming pioneer Shannon [1]. Shannon was the scientist who created the branch science known today as information theory and in his publication “Programming a Computer for Playing Chess”, which appeared in 1950, he laid the ground for chess programming and the ways it can be approached [2].

His work outlined two major paths the computer algorithms could follow:

• Type A strategy: Brute force algorithm. The chess program examines all possible moves up to a certain depth.
• Type B strategy: Selective search algorithm. The chess program examines only the plausible moves in each position in a relatively greater depth than Strategy A.

Selecting one of the two options was initially obvious. Yet, history works in mysterious ways. At the end, the obvious option died and the less-obvious one prevailed. The implications of that

Initially the pioneers of chess programming, like M. Botvinnik tried to implement the Type B strategy. The goal was anyway obvious: to emulate the mind of a chess master, who in any given position immediately recognizes the most plausible moves and examines only those in a great depth. Moves that are obviously useless or irrelevant to the position are not considered at all.

That seemed like the most logical path to follow, since computer programming’s initial goal was to emulate the way humans think and not to just search for every possible move and compute the game up to the end. However, this path was doomed from the beginning due to the lack of computing strength at the time.

Botvinnik’s research on chess-playing programs for example, concentrated on “selective searches”, which used general chess principles to decide which moves were worth considering. This was the only feasible approach for the primitive computers available in the Soviet Union in the early 1960s, which were only capable of searching three or four half-moves deep (i.e. A’s move, B’s move, A’s move, B’s move) if they tried to examine every variation. [3]

This approach has (had) severe drawbacks. The selective search would produce blunders every now and then; for too often for any computer program that wants to be considered competitive.

For a “best move generator” to be any good, it has to be almost perfect.  Even if a program is equipped with a function that looks for the 5 best moves in a position, and that the objective best move is among those 5 at least 95% of the time, the probability that the generator’s list will always contain the best choice at all times, during a 40-move game, is less than 13%.  Even a generator with 99% accuracy will blunder at least once in about a third of its games. [4]

Since the computer strength has been increasing exponentially for the past 60 years, the Option A was the way forward for chess programming. It was clearly painful for Botvinnik that a rival Soviet program, KAISSA, was far stronger than Pioneer he had created, and had, in fact, become the first world computer chess champion in 1974. Kaissa was a pure brute force program. [5]

Brute force searches were later optimized with various methods, like alpha-beta pruning. [2] These improvements made the brute force algorithms more quick and efficient and the obvious choice for any chess program. And thus, the story was over, the path was selected. And computer chess would continue walking in the same path for years to come, up until today.

Option A: The computational option – Brute force

Shannon’s Option A used brute force to find the best move. The algorithms using this option essentially explore all possible legal moves in a position and then evaluate the positions resulting after those moves.

The process is re-iterated for the search depth defined in the algorithm and then the results are sorted and processed so as to find the best move in the initial position.

One of the most known ways to sort the analysis results and get to the best move, is the MinMax algorithm. According to that method, the computer, after having calculated the full ‘tree’ of possible moves for a given initial position, it then propagates from the deeper level (i.e. the maximum depth reached) back to the initial position by selecting the best move for the computer or for the human opponent at each thinking depth level.

The MinMax algorithm

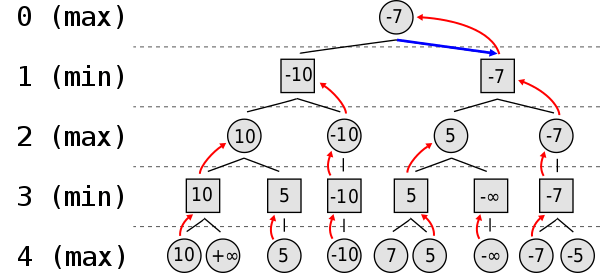
MinMax algorithm diagram by Nuno Nogueira (Nmnogueira), retrieved from Wikipedia article on MiniMax algorithm, shared under CC BY-SA 2.5 license (source)

The chess algorithms today are based in one way or the other on a well known von Neumann’s theorem. The von Neumann’s minimax theorem about zero-sum games was published in 1928 and is considered the starting point of game theory. [7]

The two essential parts of von Neumann’s 1928 paper are the mathematization of “Gesellschaftsspiele” or “games of strategy” and the proof of the theorem “Max Min = Min Max” for a game involving two players who play against each other and for which the players’ gains add up to zero. [8]

What MinMax says in simple words, is that in a zero-sum game like chess, each opponent tries to either maximize or minimize the score. So for example in chess, if a positive score is good for white and a negative is good for black, one player will try to increase the score while his opponent will try to do the opposite. When the chess algorithm analyzes the moves’ tree, it will have to consider both these goals of the two opponents and, thus, will analyze the tree by alternatively finding the moves that maximize or minimize the position’s score depending on who plays, thus the term MinMax algorithm. [2]

This is however only part of the story. The other very important part, is how to select which moves to analyze with that algorithm. Is the system going to analyze them all up to a specific depth (Option A) or is it going to be ‘clever’ enough to find only a selected set of good moves to analyze at maximum depth? (Option B).

Option B: The human option – Selective search algorithms

As mentioned above, the option that was initially one of the most logical ones was the option where the computer finds the most plausible moves and analyzes only those.

The benefits of this option are that the computer does not need to search for all moves and, thus, can think faster and more efficiently. The main drawback and already mentioned, is that the algorithm easily misses good moves and can easily blunder, if in the given position it cannot find with success the most plausible moves.

One of the first algorithms that attempted to implement Shannon’s Option B was the one created by M. Botvinnik and used by the Pioneer chess computer.

Botvinnik’s algorithm utilized the notions of trajectories and zones. The concepts of zones as intermediate level of the MP consists of a network of main trajectories conform to attacking or defending plans determined elsewhere, negation trajectories, that is opponent’s counter trajectories which may block or combat the primary trajectory in time, and own supporting counter-counter trajectories. The MP controls the growth of a search tree inside a best-first search, and prunes all branches forward which could not reach a goal in time. [6]

Where are today’s computers?

Most of the chess computers and chess programs of today implement Option A, with some modifications that made the search more efficient.

However, there are noticeable exceptions.

AlphaZero is one of them. This chess engine was a neural network based chess engine that learned how to play chess in a matter of a few hours after playing with itself. It then managed to play with the strongest chess engine of the time, Stockfish, and prevail in an astonishing way.

AlphaZero played a test match against an open source engine named Stockfish, one of the top three or four brute force engines in the world. These programs all hover around 3500 points on the rating scale, which is at least 700 more than any human player. Stockfish ran on 64 processor threads and looked at 70 million positions per second; AlphaZero ran on a machine with four TPUs, looking at just 80,000 positions per second. It compensated for this thousand-fold disadvantage by selectively searching only the most promising variations – moves that in its self-play had proved to be effective in similar positions. [9]

AlphaZero employs a technique called Monte Carlo Tree Search (MCTS). MCTS focuses on statistically promising parts of the search space, balancing exploration (trying new moves) and exploitation (choosing good moves found previously). This makes it more efficient than brute force. [10]

Here’s a breakdown of how it works:

1. Selection: Starting from the current position, AlphaZero uses a process to select the most promising move to explore further. This selection can involve factors like:
   • Win Rate: The win rate associated with a move based on previous simulations. Moves with higher win rates are more likely to be chosen.
   • Exploration Bonus: To encourage exploration and avoid getting stuck in known good moves, there’s a bonus added to moves that haven’t been explored as much. This helps uncover hidden potential in less-trodden paths.
2. Simulation: Once a move is selected, AlphaZero simulates the game forward from that position using a simpler, faster evaluation method. This simulation can be a self-play scenario where AlphaZero plays against itself, or a pre-defined set of rollout policies.
3. Backpropagation: After the simulation ends with a win, loss, or draw, the outcome is propagated back up the tree. This updates the win rates and exploration statistics for all the moves involved in the simulation path.
4. Iteration: This process of selection, simulation, and backpropagation repeats for a set number of times. As more simulations are done, the win rates and exploration statistics become more accurate, guiding AlphaZero towards the most statistically promising parts of the search space. [11]

This method seems closer to Option B. The algorithm tries indeed to find the best possible moves in the position. However, the way this is done raises question regarding the true nature of the option used. (there are of course no questions regarding the effectiveness of the algorithm)

Do modern chess computers know they are using Option A?

In the movie “Ex Machina”, a computer programmer was summoned by a technology company tycoon to test an artificial intelligence robot he had created. After having spoken with the robot the programmer was really amazed. In his own words, he thought it was ‘f***ing amazing’. But one morning he was still thinking. And was trying to find out if what he was doing, i.e. speaking with it, was the right way to test it.

According to the hero of the story, there was something wrong with testing a talking robot by talking to it. It was like “playing chess to test a chess computer” as he said. “How else would you test a chess computer?” the tycoon asked. “Well, you can play chess and see if it makes the right moves. But that will not tell you if it knows it plays chess, or if it knows what chess is” the programmer answered.

That is a surprisingly intuitive and simple question.

And, thus, a hard one to answer.

Here I will not try to answer if AlphaZero knows it is playing chess. It does not. Computers are far from having consciousness so this is not the question we should focus for now. My question is a more basic one: Does the AlphaZero algorithm implement the Option B of Shannon or is it an Option A in disguise? Do its programmers know they are utilizing Option A regardless of how well they try to conceal it?

The question can be answered only if we search the foundations of the algorithm: Does it rely on chess principles to find the best possible moves? E.g. does it search for moves that maximize the mobility of the pieces of the computer or does it seek moves that minimize the danger to the pieces of the computer? Does it seek moves that result in controlling the center or does it search for moves that result in open positions when the computer has a bishop?

Let’s see what Google Gemini answers to that.

Question: Does this algorithm (i.e. the Monte Carlo Tree Search) utilize specific chess strategic principles to properly rate each move?

Answer: No, AlphaZero’s algorithm does not rely on pre-programmed chess strategic principles to rate moves. Instead, it leverages a technique called deep neural networks to evaluate positions and select moves.

Here’s a breakdown of how it works:

• Deep Neural Networks: AlphaZero is trained on a massive dataset of past chess games. This dataset serves as a learning experience for the neural network, allowing it to identify patterns and relationships between board states and winning outcomes. Over time, the network develops its own evaluation function, essentially figuring out which moves are more likely to lead to victory.
• Move Selection: During gameplay, AlphaZero utilizes a Monte Carlo Tree Search (MCTS) to explore different move options and predict their outcomes. MCTS simulates many possible game continuations for each candidate move, relying on the neural network’s evaluation to determine the most promising path.

In essence, AlphaZero learns by playing against itself millions of times. Through trial and error, it discovers successful strategies and tactics without needing explicit programming of chess principles. [17]

AlphaZero chess algorithm

The AlphaZero chess algorithm is summarized in this section. This summary aims at making it clear if and whether the the algorithm actually plays good chess because it applies good solid chess principles, or if it is all a matter of statistical analysis. (Note: The latter is proved true)

Step 1: Neural network nnet0 is initialized

The network returns two randomly generated outputs:

• v(s): Win probability of the player from position s
• p(s): Contains how promising each of the legal moves from position s is (policy vector)

This initial network will be used to train subsequent networks to play better, a process that will be repeated multiple times until specified.

Step 2: Run simulations for every move

On every move s, a number of simulations are run. Each simulation entails executing the following algorithm until the first position that has not been visited by any of the previous simulations is encountered:

Step 2.1: Select the most productive move

Out of all the legal moves in the current position, select the most productive one. (i.e. the one that has the perfect balance between exploration and exploitation). This is the move that maximizes the upper confidence bound.

The upper confidence bound is a function of Q (exploitation score), P (indication of how promising a move is) and N (number of times a move has been visited from position s) [16]

Step 2.2: Play the selected move until a certain point

Play the selected move and run the algorithm again until…

• the end of the game is reached => the exploitation score Q is recalculated for the move OR
• a position r that has not been visited by any previous simulation is encountered => Calculate P for position r (i.e. the policy distribution that contains how promising each legal move is in position r). How this calculation is conducted is not publicly available; there is a possibility that this is done either randomly initially or based on a very basic evaluation function.

Once the pre-selected number of simulations have been completed, the policy distribution is created. That distribution contains how many times each of the legal moves in position s has been visited.

Note that the second neural network output is completely random, since it is based on the output of the first neural network that was also random.

Step 3: Play against self to create data for training a new model

Get the network created playing against itself a large number of times so that it can be trained. The moves played in these games are based on the policy vector that shows which moves are the most promising, however an element of randomness is injected in the process so that the network does not choose the same moves all the time.

This self-play will generate the needed data for the algorithm to create the next and, hopefully, more advanced neural model in the next step of the process.

Step 4: Create a new network nnet1

A new network nnet1 is created based on the input from the old one (nnet0) and self-training it conducted.

AlphaZero uses a technique called experience replay. Here, past experiences from self-play games are randomly sampled and used to train nnet1.

The valuable information for nnet1 comes from the entire self-play experience of nnet0, not just a single updated policy vector. This experience includes:

• The game state (position) at various points.
• The move nnet0 chose based on its policy.
• The final outcome of the game (win, lose, or draw).

Step 5: Make sure the new network is better than the old one

Since the first neural network was completely random, the second neural network will also output a completely random policy estimator, as it will have been trained on that initial random input (policy vector). However, from the third neural network onward, the outputs should start becoming more meaningful, getting more accurate with every new generation.

To make sure that happens, the algorithm makes the old neural network and the new neural network play against each other. From the result of the games between the two networks, the algorithm can then realize whether the second network is better than the first one. If yes, then the second network is used. If not, the first network is used. [16] [18]

Note: The specific details of the neural network architecture and the learning algorithms used in AlphaZero are not publicly available.

Playing good chess without knowing chess

As it was evident from the above sections, AlphaZero played super-strong chess without having any knowledge of any chess principle whatsoever.

Such a conclusion is not a startling one. Someone could have guessed it by simply looking at how successful the algorithm applied to AlphaZero in chess is to other games as well, like Go for example. [15] [16] An method that can have so amazing results in such a broad range of games cannot be relying on specific principles for each game per se. Well, it could to be honest, but that would require a tremendous amount of time and expert effort to optimize the engine for one specific game only. And we know that the specific method was applied consecutively in multiple games and with the same stellar results.

The fact that an algorithm can play good chess without any hardcoded chess principles raises some interesting questions.

What does it mean to lose from a computer using such an algorithm?

Could we also use such an algorithm as humans? And if we did, would that mean that we play good chess? Even worse, do we perhaps already use such an algorithm without even knowing it?

If an algorithm can produce excellent results regarding a specific game without knowing anything for that game, what does that tell us about the very nature of knowledge regarding that game? If we can play chess perfectly without knowing chess principles, does that mean that perhaps we could master other areas of knowledge as well without any knowledge of them?

(Isn’t that what we already do? Any knowledge field we have conquered to-day, was once a dark place for which we knew nothing before…)

Chess and Philosophical implications

The way chess programming research has been progressing lately, there is little hope that we could change the selected option (i.e. Option A disguised as a clever Option B) any time soon.

Why is this bad though?

First of all it is bad because the brute force option does not offer incentives to invest more into the qualitative elements of the game. Chess scientists become ‘lazy’ and do not really care about making breakthroughs in the evaluation of positions or in finding new ways to analyze the game, since relying on brute force statistical analysis produces results.

In the same way, Artificial Intelligence could face similar issues in other areas of research as well. Beyond chess, there is a whole world of AI that delves into any known facet of human civilization. From documents and data analysis, to comprehension of difficult abstract subjects and even artistic expression projects, AI is destined to surpass us in almost everything.

But how will it do that?

Could AI create perfect paintings replicating known masters or even by creating its own original style, without knowing what painting and what art is?

Such questions are even harder than the chess related ones, because, for example, in this case not even we know what art is.

But does it matter? When we see a painting, we like it or we do not like it. If that painting stirs feelings inside our soul, then it is a good painting. Does it matter how it was created? In a similar way, if AlphaZero plays phenomenal chess does it matter how it does it?

And the questions continue.

Can AI be considered as conscious even if it passes the Turing test without ever feeling the deep emotion of realizing “I am Me”? Can the AI be considered intelligent without even understanding what intelligence is?

But the answers will keep coming in.

And AI will keep on helping us.

Even though we may never accept it as equal.

Barely illuminating the path towards the last place we would consider home.

(Out of Troy, Rome was born…)

The way forward: Redefining Option B

What are the chess principles a chess program should follow? There are many articles and books trying to document the chess principles a good chess player should follow.

If we are to redefine Option B so as to make it more flexible and powerful, we should re-investigate those principles and perhaps invent new ones.

However, the example of AlphaZero (and other modern chess algorithms, like Stockfish, which use similar neural network processes) shows that perhaps the way forward is a different one. Perhaps what we should be seeking is not a refined list of chess principles but a way to play chess without any chess principle whatsoever!

In essence, that the way AlphaZero operates and plays great chess.

Principles are good up to a point. They are able to give your play structure and can support your attempts to formulate plans. But any path taken obscures the way towards other paths, potentially more promising.

If AlphaZero can win games by sacrificing pieces in the beginning of the game, by playing the same piece twice in an opening or by placing the king on e3 from the initial stage of the game [19], then why would we ever need chess principles to guide our chess computers?

Non-thinking as the conclusion

Humans have been viewing thinking as the main characteristic defining them as superior to other beings. We think, therefore we exist. We think, therefore we can create civilization, create tools and examine philosophical questions.

But what if we were to follow the AlphaZero example?

What if non-thinking is far more powerful than thinking?

It is true that thinking has helped us immensely throughout human history. It is because of thinking that we have managed to be where we are today. But what if non-thinking could get us even further?

We have experienced cases where people discover great mathematical conjectures ‘out of the blue’, where scientists found the solution to problems in dreams (Pauli), where instinct and intuition have served us more than structured and principles-based organized thinking.

Are we brave enough to explore this dark path?

Think about it.

(Or rather, don’t…)

Resources

[1] Iryna Andriyanova. 100 Years of Shannon: Chess, Computing and Botvinik. Doctoral. United States, 2016, https://hal.science/cel-01709767/document.

[2] Brudno, Michael (May 2000). “Competitions, Controversies, and Computer Chess” (PDF). Retrieved 2008-11-18.

[3] Mikhail Botvinnik Wikipedia article https://en.wikipedia.org/wiki/Mikhail_Botvinnik. Retrieved 2024-05-12.

[4] Laramée, F.D. (July 2000). “Chess Programming Part III: Move Generation”. gamedev.net. Archived from the original on 2009-02-12. Retrieved 2008-11-18.

[5] The Adventure of Chess Programming (Part 2), Frederic Friedel, https://en.chessbase.com/post/the-adventure-of-chess-programming-part-2, retrieved on 2024-05-12.

[6] Pioneer chess program, https://www.chessprogramming.org/Pioneer, Retrieved 2024-05-12.

[7] Minimax theorem Wikipedia article, https://en.wikipedia.org/wiki/Minimax_theorem. Retrieved on 2024-05-12.

[8] John von Neumann’s Conception of the Minimax Theorem: A Journey Through Different Mathematical Contexts, Tinne Hoff Kjeldsen, Arch. Hist. Exact Sci. 56 (2001) 39–68, Springer-Verlag 2001, https://web.math.ucsb.edu/~crandall/math201b/vnminimax.pdf, retrieved on 2024-05-12.

[9] The Adventure of Chess Programming (Part 3), Frederic Friedel, https://en.chessbase.com/post/the-adventure-of-chess-programming-part-3, retrieved on 2024-05-12.

[10] Answer by Gemini LLM (former Bard LLM), Prompt used: “Would you say it follows Shannon’s Option A for brute force search or Option B?”, 2024-05-12.

[11] Answer by Gemini LLM (former Bard LLM), Prompt used: “How does AlphaZero find these statistically promising parts?”, 2024-05-12.

[12] Monte-Carlo Graph Search for AlphaZero, Johannes Czech, Patrick Korus, Kristian Kersting, arXiv:2012.11045v1 [cs.AI] 20 Dec 2020, retrieved from https://arxiv.org/pdf/2012.11045 on 2024-05-12

[13] Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm, David Silver, Thomas Hubert, Julian Schrittwieser, Ioannis Antonoglou, Matthew Lai, Arthur Guez, Marc Lanctot, Laurent Sifre, Dharshan Kumaran, Thore Graepel, Timothy Lillicrap, Karen Simonyan, Demis Hassabis, https://doi.org/10.48550/arXiv.1712.01815, retrieved on 2024-05-12.

[14] Lessons from AlphaZero for Optimal, Model predictive, and Adaptive control, Dimitri P. Bertsekas, MIT, retrieved from https://web.mit.edu/dimitrib/www/LessonsfromAlphazero.pdf on 2024-05-12.

[15] A summary of the DeepMind’s general reinforcement learning algorithm, AlphaZero, Umer Hasan, Medium, retrieved from https://medium.com/@umerhasan17/a-summary-of-the-general-reinforcement-learning-game-playing-algorithm-alphazero-755f1de1ce38 on 2024-05-12.

[16] AlphaZero Chess: How It Works, What Sets It Apart, and What It Can Tell Us, Maxim Khovanskiy, Medium, retrieved from https://towardsdatascience.com/alphazero-chess-how-it-works-what-sets-it-apart-and-what-it-can-tell-us-4ab3d2d08867 on 2024-05-12.

[17] Answer by Gemini LLM (former Bard LLM), Prompt used: “One more question regarding AlphaZero and its chess algorithm. I know it uses the Monte Carlo Tree Search. My question is the following: Does this algorithm utilize specific chess strategic principles to properly rate each move?”, 2024-05-12.

[18] Discussion with Google Gemini on 2024-06-02, with input the summary of the AlphaZero algorithm produced for this paper.

[19] https://www.chess.com/forum/view/general/the-most-beautiful-game-ever-alphazero-vs-stockfish